Package Exports
- @datastructures-js/set
This package does not declare an exports field, so the exports above have been automatically detected and optimized by JSPM instead. If any package subpath is missing, it is recommended to post an issue to the original package (@datastructures-js/set) to support the "exports" field. If that is not possible, create a JSPM override to customize the exports field for this package.
Readme
@datastructures-js/set
extends javascript ES6 Set class and implements main operations between two sets.
Table of Contents
Install
npm install --save @datastructures-js/setAPI
require
const EnhancedSet = require('@datastructures-js/set');import
import EnhancedSet from '@datastructures-js/set';javascript Set class
It extends ES6 Set class so it already has all the Set functionality.
https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Set
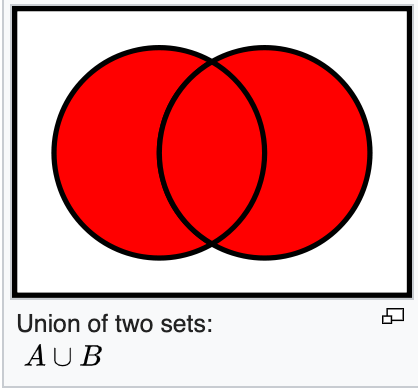
.union(set)
applies union with another set and returns a set with all elements of the two.
https://en.wikipedia.org/wiki/Union_(set_theory)
| params | |
|---|---|
| name | type |
| set | Set |
| runtime | explanation |
|---|---|
| O(n+m) |
n = number of elements of the first set m = number of elements of the second set |
Example
const set1 = new EnhancedSet(['A', 'B', 'C', 'D']);
const set2 = new EnhancedSet(['C', 'D', 'E', 'F']);
const union = set1.union(set2); // {A, B, C, D, E, F}.intersect(set)
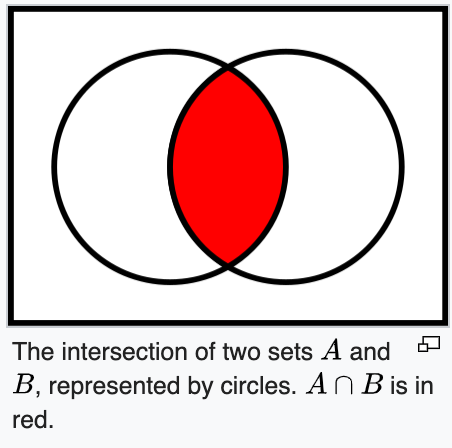
intersects the set with another set and returns a set with existing elements in both sets.
https://en.wikipedia.org/wiki/Intersection_(set_theory)
| params | |
|---|---|
| name | type |
| set | Set |
| runtime | explanation |
|---|---|
| O(n) | n = number of elements of the set |
Example
const intersect = set1.intersect(set2); // {C, D}.complement(set)
returns elements in a set and not in the other set relative to their union.
https://en.wikipedia.org/wiki/Complement_(set_theory)

Example
const set2Complement = set1.complement(set2); // {A, B}
const set1Complement = set2.complement(set1); // {E, F}.isSubsetOf(set)
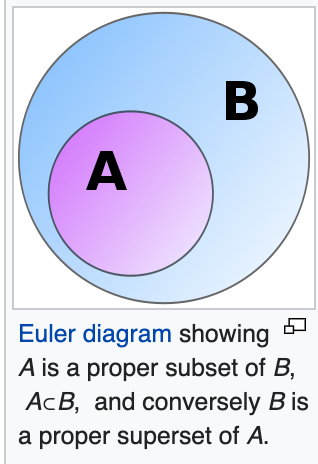
checks if the set is a subset of another set and returns true if all elements of the set exist in the other set.
https://en.wikipedia.org/wiki/Subset
| params | |
|---|---|
| name | type |
| set | Set |
| runtime | explanation |
|---|---|
| O(n) | n = number of elements of the set |
Example
console.log(s1.isSubsetOf(new Set['A', 'B', 'C', 'D', 'E'])); // true
console.log(s1.isSubsetOf(s2)); // false.isSupersetOf(set)
checks if the set is a superset of another set and returns true if all elements of the other set exist in the set.
https://en.wikipedia.org/wiki/Subset

| params | |
|---|---|
| name | type |
| set | Set |
| runtime | explanation |
|---|---|
| O(n) | n = number of elements of the set |
Example
console.log(s1.isSupersetOf(new Set['A', 'B'])); // true
console.log(s1.isSupersetOf(s2)); // false.product(set)
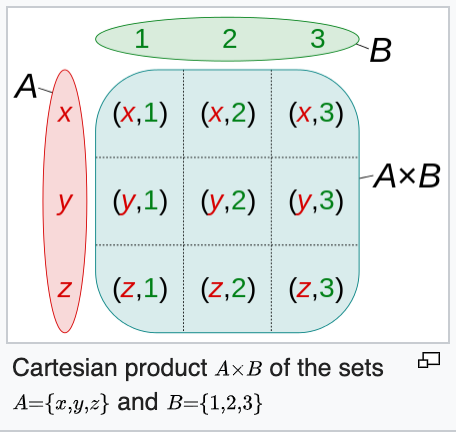
applies cartesian product between two sets.
https://en.wikipedia.org/wiki/Cartesian_product
| params | |
|---|---|
| name | type |
| set | Set |
| runtime | explanation |
|---|---|
| O(n*m) |
n = number of elements of the first set m = number of elements of the second set |
Example
console.log(set1.product(set2));
/*
EnhancedSet {
'A,C',
'A,D',
'A,E',
'A,F',
'B,C',
'B,D',
'B,E',
'B,F',
'C,C',
'C,D',
'C,E',
'C,F',
'D,C',
'D,D',
'D,E',
'D,F'
}
*/Build
grunt buildLicense
The MIT License. Full License is here


